Giriş
Matematik, evrensel bir dil ve sonsuz bir keşif alanıdır. Özellikle özel yetenekli öğrenciler için, bu alanda derinlemesine düşünme ve problem çözme fırsatları sunar. Geçtiğimiz günlerde, öğrencilerimle birlikte matematiksel örüntülerin gizemini çözmek için bir yolculuğa çıktık. Bu yolculukta bize rehberlik eden ise Wolfram Alpha oldu, bir tür matematiksel sihirbaz.
Örüntülerin Keşfi
Öğrencilerimle ele aldığımız örüntüler şunlardı:
Bu örüntüler, matematiksel düşünme ve analiz becerilerini geliştirmek için mükemmel örneklerdi. Öğrencilerim, bu dizilerin 20., 100. ve 150. terimlerini bulmakla görevlendirildi.
Wolfram Alpha’nın Rolü
Wolfram Alpha, bu süreçte sadece bir araç değil, aynı zamanda öğrencilerime matematiksel düüşünceyi ve problem çözme stratejilerini öğreten bir öğretmendi. Bu platform, öğrencilerin örüntüleri analiz etmelerine ve genel formülleri bulmalarına olanak tanıdı.
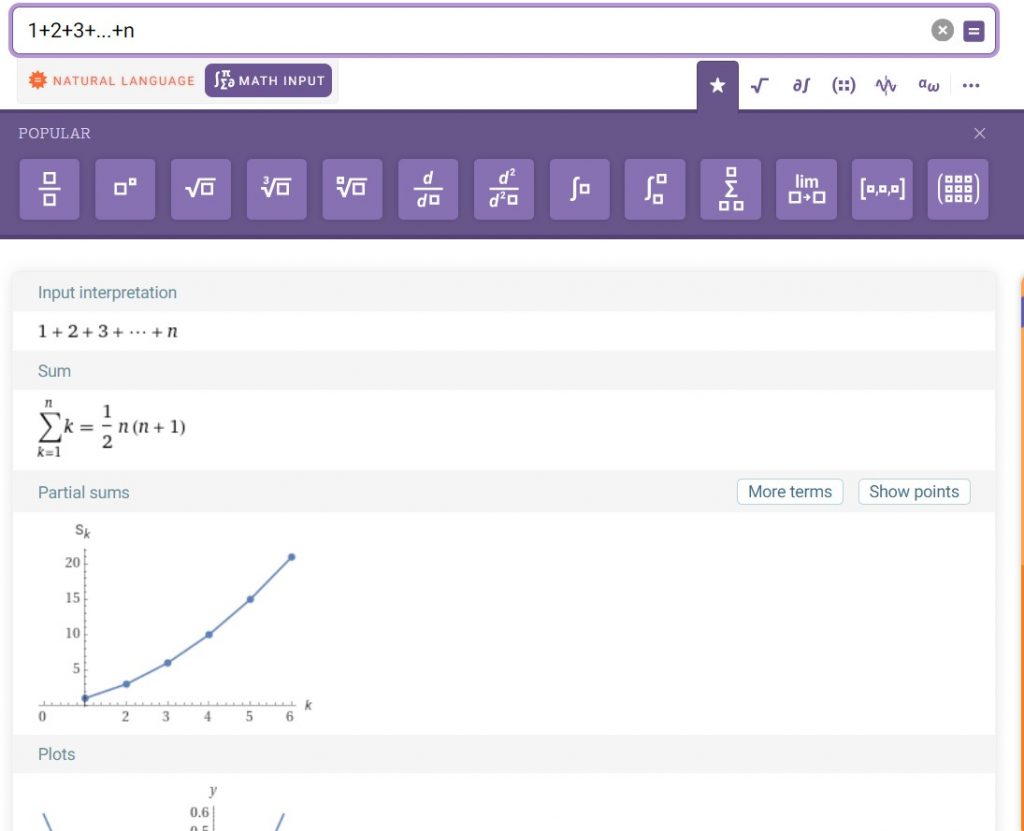
Örüntü 1: Aritmetik Dizi
İlk örüntü, basit bir aritmetik diziydi. Öğrencilerim, her yeni terimin bir öncekine 4 eklenerek oluşturulduğunu hızlıca fark ettiler. Genel formülü a_n = 3 + (n-1)*4 olarak belirledik. Bu formülle 20., 100., ve 150. terimleri kolayca hesapladık.
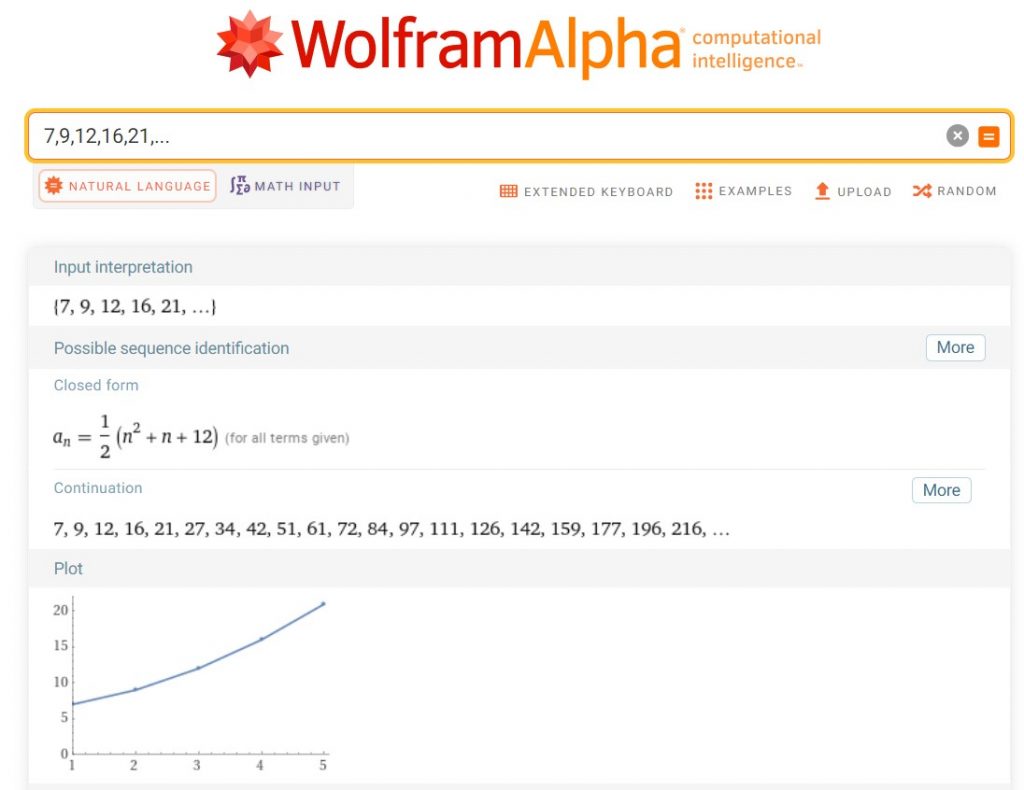
Örüntü 2: Başka Bir Aritmetik Dizi
İkinci örüntü de bir aritmetik diziydi, ancak bu sefer fark 5’ti. Genel formül a_n = 8 + (n-1)*5 oldu. Bu formülle gerekli terimleri bulmak yine zor olmadı.
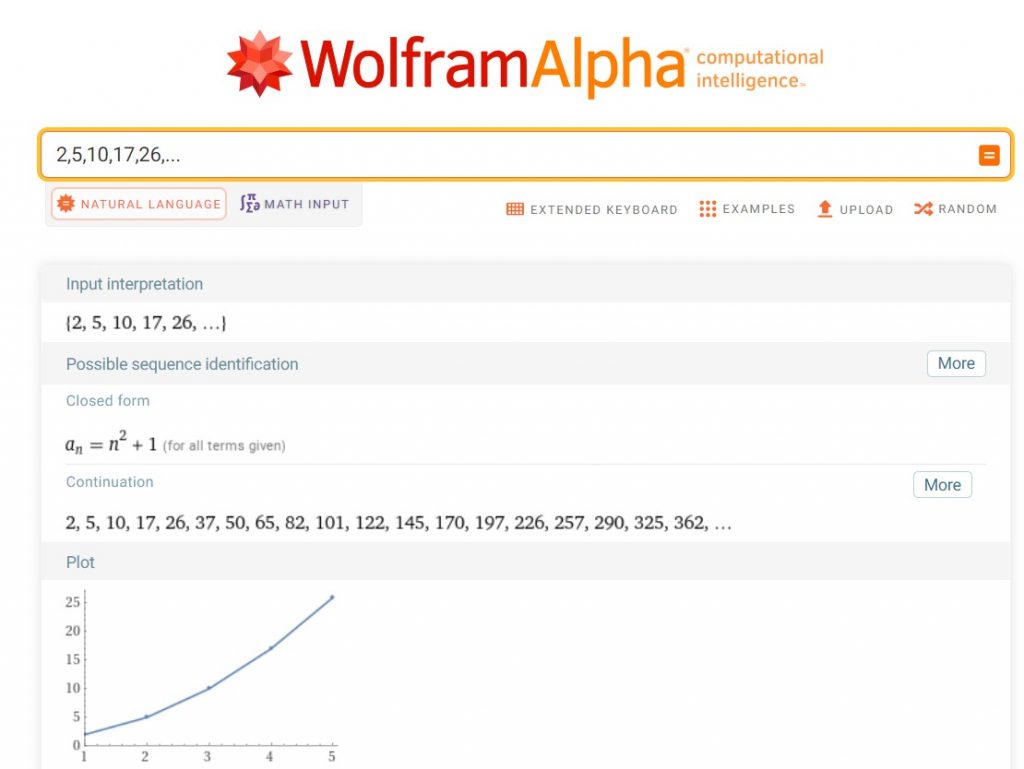
Örüntü 3: Karesel Dizi
Üçüncü örüntü, karesel bir dizi idi. Bu dizi, öğrencilerim için biraz daha zorlayıcıydı, çünkü her terim bir öncekinin karesiydi. Genel formülü a_n = n^2 olarak belirledik. Bu formül, öğrencilerimin kare alma ve cebirsel düşünme becerilerini geliştirmelerine yardımcı oldu.
Sonuçlar ve Öğrenme Deneyimi
Wolfram Alpha’nın yardımıyla, öğrencilerim bu örüntülerin 20., 100. ve 150. terimlerini başarıyla buldular. Bu süreç, onlara matematiksel düşünme, formül geliştirme ve teknolojinin matematik öğreniminde nasıl kullanılabileceğini gösterdi.
Son Düşünceler
Bu deneyim, özel yetenekli öğrenciler için matematiksel düşünmenin sadece kağıt ve kalemle sınırlı olmadığını gösterdi. Wolfram Alpha gibi araçlar, öğrencilere daha geniş bir perspektif sunarak, matematiksel düşünceyi ve problem çözme becerilerini geliştirmelerine yardımcı oluyor. Öğrencilerim bu deneyimden büyük keyif aldı ve matematiksel keşiflerinin sınırlarını zorlamaya devam etme konusunda daha da heveslendiler. Bu tür teknolojik araçların eğitimde kullanımı, öğrencilerin öğrenme deneyimlerini zenginleştirmenin ve onları geleceğin zorluklarına hazırlamanın anahtarıdır.